“I want to do the imagining, not be the idea. I want to be part of the people that make meaning, not the thing that’s made.” (Barbie)

College application deadlines are fast closing. With another year, another season of new programmers is seeking to join a field where most of us are still asking “will we even need programmers a year from now … five years from now … or ten years from now?” Though it’s died down to a simmer, the existentialism of early 2023 remains, leaving new coders and industry professionals alike wondering whether Large Language Models, such as OpenAI’s Chat GPT, will start taking over our code-writing jobs. Whether you’re someone who is pushing the application deadline in the hopes of starting their career, someone who has been coding for a long time, or even a New Year’s resolution coder, I’d like to propose that we step back and reflect … with a little help from Barbie.
Early last year, our industry entered into a period of eschatological reconning, flooded by reflections such as this one and this one. Just a few months later, we saw a flurry of tools introduced that promised to make good on these fears. In the summer, OpenAI published updates for structured output, making it a more powerful, consistent option for generating code. Vercel’s v0 system, ostensibly, allows you to create production-ready React code just by describing what it should look like.
For some reason, though, the “learn to code” movement progresses un-phased. Earlier last year, Code.org published its proposal to see Computer Science standards made a fundamental requirement for high school graduation. Several states have already made the move. This push is supported by a plethora of kid-friendly coding tools: Scratch, Tynker, and Hopscotch, just to name a few. Upping the ante, back in October, the fine folks at the MIT Media Lab’s Lifelong Kindergarten team launched OctoStudio. It brings the block-based Scratch programming language out of the browser and straight to a new generation of potential coders, on their mobile phones. It’s a fantastic system that sees the idea that “kids should learn to code” echoing on, as a resounding, self-evident mantra. But in a world where machines are getting really good at writing code, is this still valid advice?
Whatever your situation, I’d like to make a recommendation. Whether you’re a student yourself, working in education, or a professional engaged in continuing education, I’d like to recommend that you stop and take a moment. What if you didn’t learn to code? What if, instead of learning to code, you learned to model?

What’s a Model, Anyway?

A model is a symbolic representation. It is a relationship between two systems. A system is just a collection of things that have relationships with each other. The “things” are sometimes called nodes or actors. Given a model system, you can be sure to find corollary nodes and relationships in the system that it models. Therefore, a model says “this thing is this other thing,” or at least represents important parts of it.
As kids, my siblings and I built model cars with our father. These little, plastic simplifications held a symbolic relationship with their life-sized namesakes by sharing important features in common. In this case, it was the colors, shapes, and relative sizes of certain exterior components. By looking at the model, you are sure to be able to picture, understand, and predict the same features in the modeled system. If my model is red, the car it models should be red, too, and so on. This definition holds for every place we think of the word model. Even supermodels are offered up as symbolically representing what the typical or ideal human should look like. (Whether or not the modeled system in this case actually exists is another problem … but we’ll get to that in a moment).
Thankfully, you don’t have to get your fingers glued together or go on a weight-loss plan to model. We’re all modeling, every moment of every day. You might say that we can’t help it.

This is your brain, modeling…

The basis of intelligence is memory, and memory is, itself, a model. When a certain combination of stimuli enters our bodies, they inspire the activation of networks of connected neurons. Those neurons can grow closer together or further apart, making the firing of that particular pathway more likely the next time those stimuli (or something sufficiently similar to them) cross our sensory radar. This growing closer or further occurs, for all intents and purposes, mechanistically, based on the presence of certain chemical hormones. These are, in turn, released in what should be a relatively deterministic pattern in response to other stimuli, usually the acquisition of some desirable internal state (food, reproductive processes, etc.). In his book Grasp, Sanjay Sarma calls this the “foundation” of our cognitive hierarchy and is used as the basis for certain approaches to psychology, such as operant conditioning.
Think about what this means for a moment, though. That means that there is an original system somewhere out there in the universe — a shiny car, a human being, a bear, it doesn’t matter — that is being modeled. There is, then, a model system — a collection of networked neurons inside of our skulls that connect to one another and fire in relationships that are directly correlated with the features and relationships in the original system. You don’t need to learn how to model, your brain just does it. It’s a modeling machine.

Where things get complicated

Somewhere along the line though, we started doing something … odd. We started making other models, external to our own minds, that represent the network of relationships that exist within our minds. We do this for a variety of reasons, though the simplest is probably communication. The rough picture of a bear or some other predator, by conjuring the notion of its presence in another mind, is useful for survival. It doesn’t take much to accomplish, either. The close visual likeness of something is usually enough to trigger the same internal model (in the form of a network of representative neurons) in someone else, provided they’ve had sufficient sensory experience to build a model corresponding to those stimuli. If we’ve both seen a bear, and I show you a photograph of one, it’s more than likely you’ll have a feeling of recognition, conjuring in your consciousness all of the same features of that bear you’ve collected in your experience — fluffy, brown, cuddly, you name it. Sometimes this little neuronal dance doesn’t work quite like we’d hoped. The study of this particular phenomenon is what we call semantics.
We have a lot of neurons in our brains, though. Their potential number of connections is used as a back-of-the-napkin estimate for the number of distinct networks, or models, they can create. It’s a lot. So, drawing a picture for every one of them became tedious after a while and we started writing things down. (That’s an oversimplification … another topic we’ll get to in a moment). Take, for example, the following paragraph:
The text
In the course of reading this paragraph, each of the words you read, as well as their carefully crafted order, was enough to trigger a dizzying series of networking connections. Each of your models for the following creatures should have been activated:
The situation model
I’m not sure what comes to mind when you read this paragraph, but it should have also conjured a series of models — your corresponding neural pathways — relating to the properties of these creatures. Now we know that there is a corresponding system. It has two things in it: a dog and a fox. The fox possesses the properties of being both brown and quick, while the dog apparently possesses the qualities of laziness. While “laziness” might seem like it breaks our model thus far, it really doesn’t. “Laziness” is simply a symbol that we’ve assigned to experiences that are, originally, sensory stimuli. These include the sensation of annoyance when a teammate is less-than-proactive, the sights that are associated with individuals labeled as such — usually synonymous with “slovenly” or “unkempt” — and the feelings induced by social pressure and conditioning that “laziness is bad.”
What we just constructed is what Daniel Willingham refers to as the context model, and it’s a powerful skill that humanity has developed. We’ve taken a model (the combination of neurons representing the situation I observed), converted it into another model (the symbols in the text above), and used that to conjure yet another model (the combination of neurons representing the situation that exists in your mind). Phew!

Playing Telephone

It’s an understatement to say that this is an impossibly complex process. With all of that complexity, you can start to see where problems might arise. For instance, you might have a very different model representing your accrued experience with small, fuzzy brown things. When I show you that bear photo, it might not contain attributes of bears that exist in my model. If your models lack, for some reason, the attributes implying potential danger, we might be in trouble. This is relatively easy to get over when our models are grounded, that is, based on first-hand sensory stimuli. All I have to do is expose you (by way of a YouTube video, hopefully) to sights of what happens to people when they get too close to bears. Semantics ain’t so hard after all.
No, where we get into the most trouble is where our models aren’t grounded directly in sensory stimuli, but constructed as a house of cards — models built from the external representation of other peoples’ models. This is the premise of the classic game of telephone, where a line of people each whisper a word in each others’ ears, from one end of the line to the other. The words spoken by the first person in line might become horribly mangled by the end, all by the slight divergences in the relationships between auditory stimuli and the neuronal maps they invoke.
Quite insidiously, we just played this game. You read the sentence “the quick brown fox jumped over the lazy dog.” However, you have no sensory stimuli for this particular system. All you have is a collection of models associated with each element in the scene, such that the composition of each thing (the dog and the fox), their properties (laziness, quickness, browns), and their respective relationships (jumping, relative speed, one being “over” the other) are conjured. Each are immediately filled in such that the model of this system now exists in your mind.
This is important: There never was a dog and there never was a fox. There is no root sensory stimuli, some actual, out-there-in-the-universe system that corresponds to this particular model. Nevertheless, the model of that system exists in your mind and mine. It’s a very long game of telephone, so long and so convoluted that it has us building models of things that never existed.

Building Better Models

These sorts of models are built very easily in environments where a lot of words get thrown around. Unfortunately, this implies their prevalence in every social endeavor. Humans are, after all, unique in the amount of time they devote to building these kinds of external models. In contrast with a photo of the bear, the models we just described are ungrounded models, and they’re all over the place: in country clubs, religions, political rhetoric, and Medium articles (😉).
Because we often want our models to be “accurate” (that is, corresponding with the real world and the things we might experience in it), we’ve invented all sorts of ways to make better models — ones that are more resistant to the telephone game. For instance, we created a symbolic language that carries within it a means of verification — a way of taking that model, going out into the world, and making sure that it corresponds with the same system we encounter. That language is mathematics, and it’s been used effectively by humans to communicate verifiable models for a very long time, starting with arithmetic and the accounting of physical objects. We use it to communicate the relationships between items in our model, with the assertion that those relationships will hold true when you go to examine the pieces of the original system. However, there are certain aspects of the original system that aren’t easy to share in mathematics.
For instance, every system worth modeling exists in the stream of time. That is, we can say that as time progresses, some properties of the objects in our original system will be different if you tried to measure them at one point as opposed to another. The classic physics example is an object in free-fall, where the distance of the object from the ground changes over time. We experience these changes viscerally when we observe a system directly. However, when we describe the relationship between these two states using mathematics, the models we share (though rigorous) don’t intuitively convey these changes over time.
The solution to this problem is to build models whose properties, themselves, change over time. This helps us build models using sensory experiences that are much closer to the experiences we would have by observing the target system. We run scientific experiments using representative samples, test cars and wings inside of wind-tunnels, and build scale models of buildings, engines, and dams. We do this all under the assumption that the behavior of these smaller nodes, their properties, and relationships is representative of those in the target system. We often build these systems to communicate to others about the way the universe works. However, their presupposed similarities to their target systems allow us to go even further, making discoveries about the behavior of the target system, given discoveries about the model. We can readily identify these kinds of models in the computer world: simulations.
Computer software is a modeling medium par excellence. It provides (mostly) for the rigorous, verifiable relationships conferred upon it by the language of mathematics, while allowing its constituent pieces to evolve, change over time, and even influence their environment. Better yet, because of its deterministic underpinnings, every single one of these models is (hypothetically) reproducible, making our telephone game that much easier to avoid! What an accomplishment!

Models, Nails, and Hammers

Not every system is a nail. Therefore, not every system requires modeling using a hammer. Not every system needs to be modeled using the rigorous, imperative flavor of a programming language or the total descriptiveness of a simulation. Sometimes it’s fine (and more efficient) to use those fuzzy models we conjure when we use spoken or written language. If you’re not playing telephone, have easy access to verification, or are participating in a low-stakes activity, it usually isn’t worth it to be so explicit. Going further, emotional models are used to represent and conjure in others sensations that accompany certain internal states. These are exceedingly difficult to create using dry mediums such as coding languages. Therefore, we bring in completely different libraries of symbols — my personal favorite being musical ones. The types of models we create are as diverse as the systems we represent with them.
In his book The Model Thinker, Scott E. Page lists a whole slew of reasons why we might create models. Generally, the models we create are determined by the outcomes we would like to achieve. Some models are only “good” within a narrow range of contexts. In his book on algorithms, Steve Skienna refers to this range of contexts as a scale. He relates a humorous, though anecdotal example with flat-earthers. It’s not a great model if you’re looking to make predictions about the movement of stars, rockets, or satellites. However, if you’re looking to build a house and make predictions about its future stability … the flat earth model works just fine.
In fact, the domain of algorithms, found at the intersection of math and computer science is particularly interesting as a modeling discipline. It contains libraries of fantastic solutions to problems both common and uncommon. It does so by focusing its effort on a very small set of generalizable data structures. Don’t let terms like “generalizable data structures” scare you off, though. These are certain families of “nodes” with very specific relationships. They’re “generalizable” in the sense that the nodes themselves don’t have many properties. This makes it easy, when we go to build a model of something, to use them as symbols in our new system to represent the objects in our target system. (One might argue that this is the goal of all of mathematics, though the algorithmic sciences are unique in their fundamental focus on the steps required to move one of these generalized systems into a particular state).
It is the goal of a computer scientist to be well acquainted with these modeling techniques and select the right one to solve a particular problem. George Polya, in his book How to Solve It, refers to this process as “making an analogy.” It isn’t unique to computer scientists — Polya was a mathematician. On the subject of theoretical physics, Richard Feynman once said that “every theoretical physicist who’s any good knows six or seven different theoretical representations for exactly the same physics.” I don’t know about you, but when I hear Feynman talking about “theoretical representations,” all I hear is “models.”
This goes well beyond the technical disciplines, too. In this month’s and next month’s elections, candidates and their parties wage fierce competition using various models representing populations, their potential behaviors, and those of their adversaries. Their success or failure will be determined, in part, by their ability to judge the current state of the thing they are modeling and, once modeled, their means with which to manipulate the social system in question. Social systems, by the way, are excessively difficult to model — a point Dan Rockmore beats into the ground in his essay for The New Yorker, emphasizing the supposed inadequacy of modeling in non-technical disciplines.

Stocking the Shelves

“Difficult” doesn’t mean impossible, and it certainly doesn’t mean it isn’t worthwhile. Modeling is possible and inevitable, in varying degrees of rigor, in every discipline. What makes the difference between the vaunted reliability of models in the hard sciences and the derided inadequacy of mathematical models in political science is, to borrow Skienna’s phrase, a matter of “scale.” I don’t mean the scale of the thing being modeled, I mean the scale of the model itself. The closer our model comes to resembling the thing it claims to represent, the more reliably we can communicate about, predict, or manipulate that original thing.
It is, therefore, the fundamental similarities between our model and its target system that determine how we use it. In the hard sciences, it might be a serendipitous coincidence that the thing we chose to model with — mathematics — shares non-trivial similarities to the thing we’re modeling — physics — and therefore explains its concise, predictive power.
We just can’t do this in the social sciences. With an estimated 86 billion neurons in the human brain, our resources are expansive. However, they are inherently limited. In the social sciences, one studies systems whose every element has just as many neurons in their own brain. This doesn’t leave any room for you to begin modeling their behavior in any kind of comprehensive manner, let alone their complex relationships and interactions with each other and their environment. Any model of human behavior will have to leave out immeasurably many details. We just can’t create a model big enough to be totally accurate.
However, this doesn’t mean that all is lost for the social sciences. Communities of sociologists and virologists were able to work together over the course of the COVID-19 pandemic to save lives, even if their models were incomplete or wrong in some respects. Every day, we rely on oversimplifications — “flat earth” models — in disciplines including social sciences, workforce dynamics, and medicine. We keep using them, not necessarily because of their completeness, but because of their pragmatic outcomes. In both rigorous and non-rigorous modeling, Polya’s words on the analogy hold true: “it would be foolish to regard the plausibility of (a conclusion drawn from a good analogy) as certainty, but it would be just as foolish, or even more foolish, to disregard such plausible conjectures.” More accessibly, a quote attributed to George Box says simply that “all models are wrong, but some are useful.”
This goes for all kinds of models, especially the ones that we make that live in our neurologically well-endowed skulls. We are always wrong. Sometimes, though, the models we make can help us do something useful. This is why, in his book on modeling, Scott E. Page advocates for a “many models” approach to life. Because every model is wrong, it means we can’t use one model for every situation, for every outcome we would like to affect. We need to build a library of tested, well-rounded, grounded models in each of our chosen problem domains that we can carefully choose and apply to new problems we encounter.
We need to put more tools in our metaphorical modeling toolbox. This is true regardless of the problem domain we work in. Musicians and composers hone their skills in manipulating specific combinations of symbols known to elicit shared emotional memories. Software Engineers build libraries of models using mathematical objects and the symbols found in computer code. Our ability to solve any problem depends on the depth and breadth of our models for that problem domain. It behooves us to stock the shelves of this library.

The Book Store

Expanding the depth and breadth of our modeling capabilities is the goal of education (though some use it for enforcing ungrounded models via ideological indoctrination). The problems that we encounter as individuals and as societies seem to grow ever more complex. This continues to increase the demand for educational systems that empower individuals to acquire deeper, richer models. Between the COVID-19 pandemic and the popular introduction of generative AI tools, last year, our traditional educational systems have demonstrated that they aren’t up to the challenge.
In my previous position at Phenomena Learning, we tried to address this by building an educational modeling system. Phenomena’s orienting goal is to help students “stock their shelves” by building and interacting with an expansive array of models for STEM topics using a variety of modeling modalities. Importantly, these modalities include code. We built a block-based coding language to allow for the development of rigorous, imperative models with as few frictions as possible.
The Phenomena block-based code editor
However, code wasn’t the only modality we included. We also created a mathematical modeling language, allowing prospective modelers to describe the relationships between objects and their properties using a visual, web-like editor.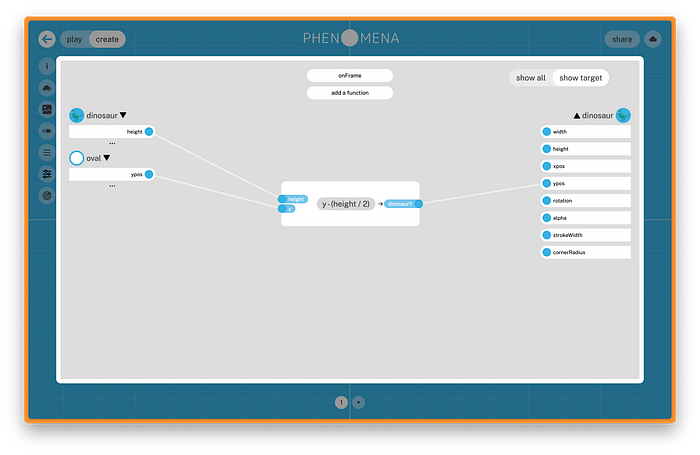
The Phenomena mathematical modeling editor
We also put a premium on the existing experience, or the lack thereof, that modelers might bring to the table. We opted for a block-based programming language instead of JavaScript to help inexperienced coders avoid syntax errors. We created a mathematical modeling language to allow students to take formulas directly from the page and put them in motion. The goal is to focus on the model, not the thing you’re using to create it. However, you don’t have to use either of these. As a drawing tool, it supports simpler, static model building as well. Much of our work involved an expanding library of “components” that can be combined as fundamental building blocks — no code required.
Though I’ve since moved on from Phenomena, the project of modeling never stops. In my current position, at Coursemojo, we’re building a system that improves on the context model, described above. It takes textual models, such as those found in English or Language Arts classrooms, and helps students to build more expansive, deeper mental models, using a conversational interface. Outside of educational contexts, I’ve written extensively about The Brain Attic, a hypothetical system that helps us connect the external models we collect in our problem domain and helps us ground (or demonstrate the ungrounded-ness) of those models. The opportunities to become better modelers are many.

The People That Make Meaning

Building this library, exercising the representations we stock it with, and refining them through iterative use is an enjoyable and rewarding activity. I can’t think of a better framing for this conclusion than Margot Robbie’s (wrongfully-Oscar-snubbed) line in the film Barbie, quoted at the top of this article. Therein, the model — the external representation of a human idea — spoke back to us, expressing a desire to be among the people who make these things instead of the model itself.
What does all of this mean for those prospective coders out there? Frankly, it’s never been enough to know how to code. Computer code, in its various iterations over the last several decades, has only ever been a medium through which we can create powerful, dynamic models. It doesn’t matter if the methods we use now are automated away in 3–5 years. There will always be a need for human beings to create well-grounded, rigorous models, regardless of the medium that is being used. It’s with this context that I often recommend to students, recent graduates, or people seeking to enter the field that it is vitally important to establish experience in a problem domain that isn’t coding. That is, instead of being “a coder,” one should seek to be “an educator that knows how to code,” or a “supply line expert that knows how to code” or something along those lines. Being “one of the people who make meaning” means that we have to have intent — understanding the system we are trying to model and what we want to do with it, as opposed to simply being familiar with the medium through which we do so.
That’s what I mean when I say “don’t learn to code” — don’t learn to code as an end unto itself. Learn to model. Collect experience in building clear distinctions between the system you are trying to represent and its environment. Recognize what type of medium you are using to make this representation. Try to be as clear as possible about your goals in the modeling process, whether that is to predict, to communicate, or to experiment. Most importantly, learn to build verifiable models, distinguishing between ones that are grounded and measurable and those that aren’t. You might do all of this using the dynamic, rigorous power of imperative programming languages. You might not. Whatever modeling medium you choose, though, build lots of them. As each of us fills the shelves of our model libraries, we’ll become that much better problem solvers. Perhaps more importantly, we’ll “be part of the people that make meaning, not the thing that’s made.”