Introduction

In the realm of machine learning, dealing with high-dimensional data poses challenges related to computational efficiency, model complexity, and overfitting. Dimensionality reduction techniques offer a solution by transforming data into lower-dimensional representations while retaining essential information. This essay aims to compare and contrast some prominent dimensionality reduction techniques, spanning both linear and non-linear methods.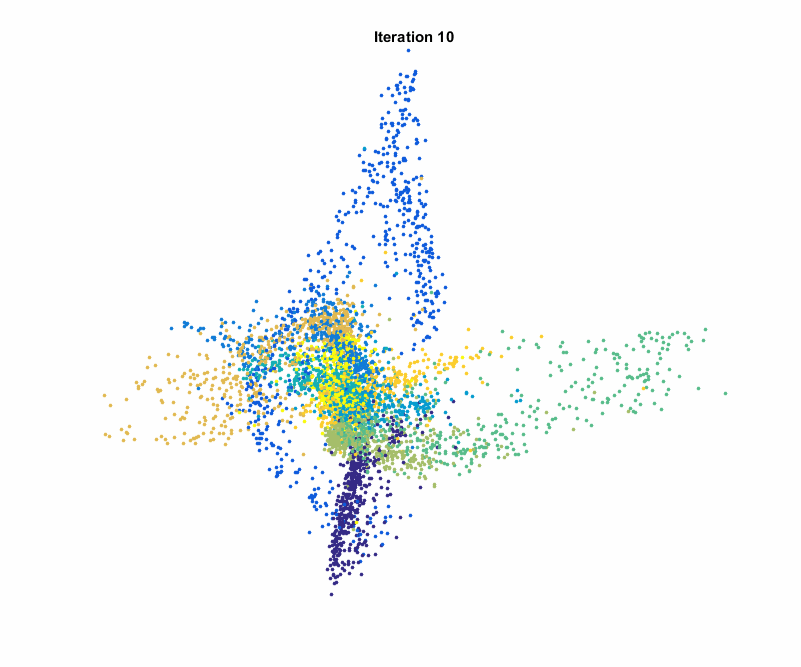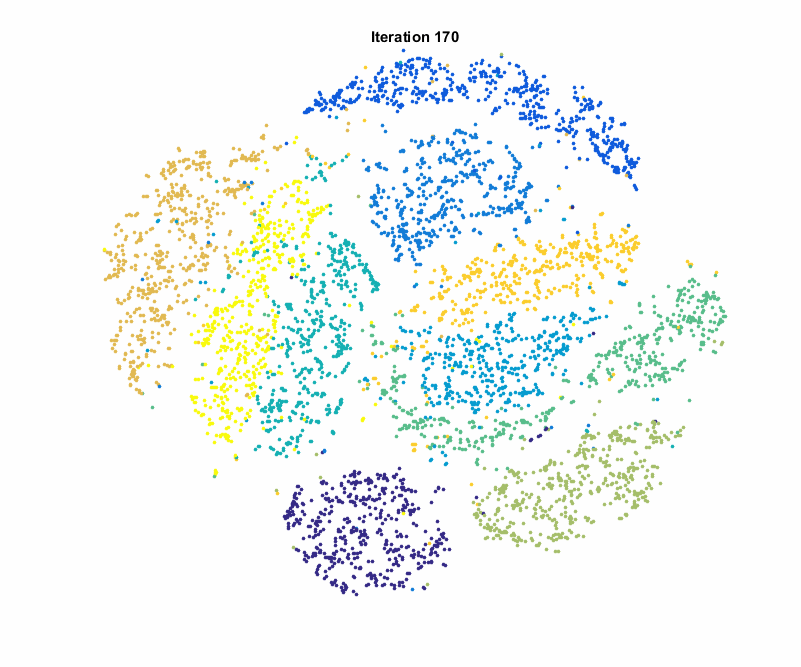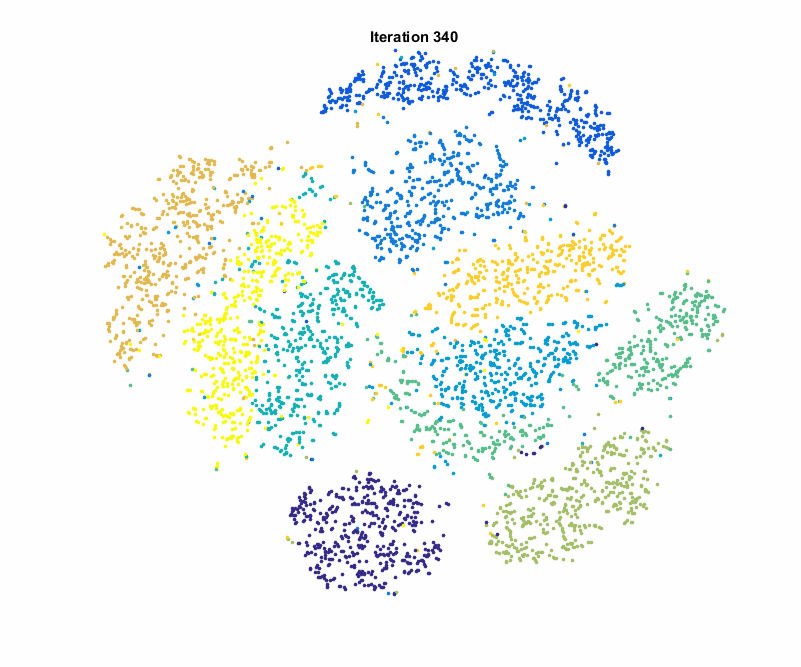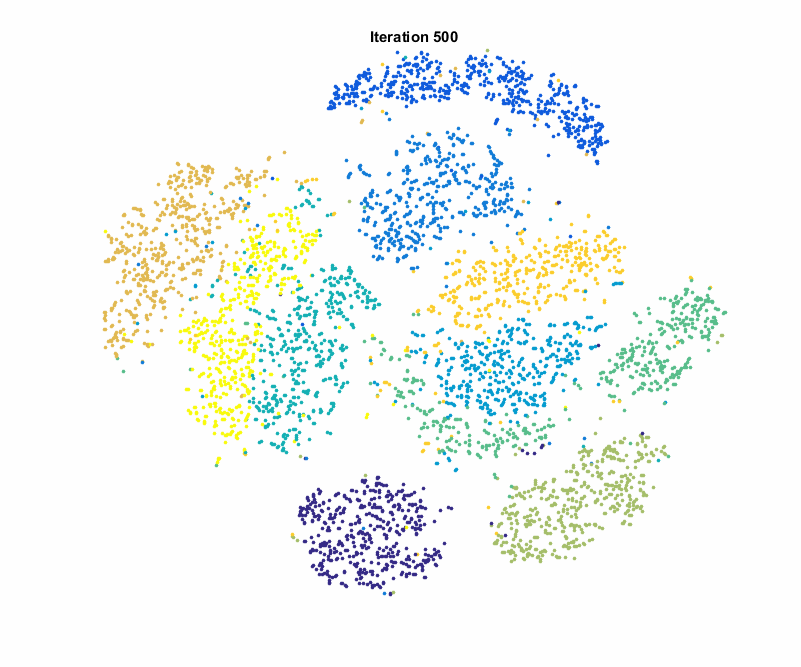


In the intricate tapestry of machine learning, the art of dimensionality reduction is the compass that guides us through the labyrinth of data complexity. Just as a skilled painter selects the perfect brushstroke, a judicious comparative analysis of dimensionality reduction techniques unveils the nuanced strokes that reveal the hidden patterns, turning the chaos of high-dimensional data into the masterpiece of insightful simplicity.

Linear Techniques

1. Principal Component Analysis (PCA)

• Linear Projection: PCA performs a linear projection to capture the maximum variance in the data.
• Computational Efficiency: Efficient and widely used, but assumes linear relationships.

1. Linear Discriminant Analysis (LDA)

• Supervised Dimensionality Reduction: LDA incorporates class information to find the linear combinations that best separate classes.
• Classification Emphasis: Particularly useful for classification tasks.

1. Random Projections

• Computational Simplicity: Random projections provide a computationally efficient method for dimensionality reduction.
• Approximate Preservation: While computationally efficient, it provides only an approximate preservation of pairwise distances.

Non-linear Techniques

1. t-Distributed Stochastic Neighbor Embedding (t-SNE)

• Non-linear Embedding: t-SNE is effective for visualizing high-dimensional data in lower-dimensional spaces.
• Computational Cost: Computationally expensive, limiting its use in large datasets.

1. Uniform Manifold Approximation and Projection (UMAP)

• Efficiency: UMAP is computationally more efficient than t-SNE, making it suitable for larger datasets.
• Global and Local Preservation: Effective at preserving both local and global structures in the data.

1. Autoencoders

• Neural Network Approach: Autoencoders use neural networks to learn non-linear mappings between high and low-dimensional spaces.
• Representation Learning: Capable of learning hierarchical representations, but may be sensitive to hyperparameters.

1. Isomap (Isometric Mapping)

• Preservation of Geodesic Distances: Isomap focuses on preserving geodesic distances, capturing the intrinsic geometry of the data.
• Sensitivity to Noise: Sensitive to noise and outliers, requiring careful preprocessing.

1. Locally Linear Embedding (LLE)

• Local Relationships: LLE focuses on preserving local relationships between data points.
• Parameter Sensitivity: Sensitive to the choice of neighbors, and may struggle with global structure preservation.

Code

Below is a complete Python code using the popular scikit-learn library to apply various dimensionality reduction techniques to the Iris dataset and visualize the results with plots. Make sure to have scikit-learn and matplotlib installed in your Python environment:


This code snippet uses dimensionality reduction techniques such as PCA, LDA, t-SNE, Isomap, LLE, MDS, Spectral Embedding, and UMAP on the Iris dataset and plots the reduced data. You can observe the different clusterings in the reduced space for each technique. Feel free to experiment with other datasets or modify the code according to your specific needs.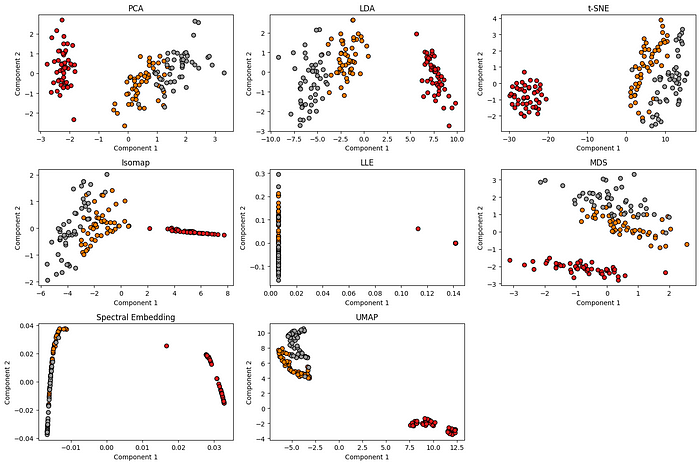


Remember to install:

Conclusion

In conclusion, the choice of dimensionality reduction technique depends on the specific characteristics of the data and the goals of the analysis. Linear methods like PCA and LDA offer simplicity and efficiency but may struggle with non-linear relationships. Non-linear techniques such as t-SNE and UMAP excel in capturing complex structures but come with computational challenges. Autoencoders provide a flexible neural network-based approach, and methods like Isomap and LLE focus on preserving specific geometric aspects. Understanding the strengths and limitations of each technique is crucial for selecting the most appropriate method for a given dataset and task, ensuring optimal results in machine learning applications.