Data Structure: The Building Blocks of Computer Science

Data structures are a fundamental concept in computer science, and they play a crucial role in how we store, organize, and process data in the digital world. Simply put, a data structure is a way of organizing and storing data in a computer so that it can be accessed and processed efficiently. In this article, we’ll explore what data structures are, why they’re important, and the different types of data structures that are commonly used.

Why Data Structures are Important?

Data structures are important for several reasons. Firstly, they provide a way to organize and store large amounts of data in an efficient manner, making it easier to process and manipulate. For example, imagine you have a list of one million names, and you need to find a specific name. If you simply stored the names in a single list, it would take a long time to search for a specific name. However, if you organized the names in a data structure like a binary search tree, you could find the name in a fraction of the time.
Another reason data structures are important is that they help to reduce the amount of time and space required to solve a problem. For example, if you want to sort a large amount of data, there are many different algorithms you can use. However, some algorithms are more efficient than others and will sort the data more quickly. By choosing the right data structure and algorithm, you can solve problems much faster and more efficiently.
Finally, data structures are important because they help to abstract away the complexities of data storage and processing, making it easier to write and maintain complex software systems. For example, instead of having to write your own code to manage the storage and retrieval of data, you can simply use a data structure like a linked list or a hash table.

Types of Data Structures

There are many different types of data structures, and each one is designed to solve a specific problem. Here are some of the most commonly used data structures:
Arrays: An array is a simple data structure that stores a collection of elements, each of which can be accessed by its index. Arrays are often used to store collections of data that need to be processed in a specific order.
Linked Lists: A linked list is a data structure that consists of a series of nodes, each of which contains a piece of data and a reference to the next node in the list. Linked lists are often used when you need to insert or delete elements from a collection of data, as they allow you to do so in a constant time.
Stacks: A stack is a data structure that implements the Last-In-First-Out (LIFO) principle. Stacks are often used to implement undo and redo functionality, as well as to evaluate expressions and perform backtracking.
Queues: A queue is a data structure that implements the First-In-First-Out (FIFO) principle. Queues are often used to process requests in the order in which they were received, and are used in applications such as printing and task scheduling.
Trees: A tree is a data structure that consists of a series of nodes, each of which contains a piece of data and a reference to one or more child nodes. Trees are often used to store hierarchical data, such as in file systems, and to perform operations such as searching and sorting.
Graphs: A graph is a data structure that consists of a collection of nodes and edges, which represent the relationships between the nodes. Graphs are often used to represent relationships between objects, and are used in applications such as network analysis and routing.

Algorithms: The Key to Solving Problems Efficiently

Algorithms are an essential part of computer science, and they play a crucial role in solving problems in a variety of fields, from mathematics and engineering to finance and medicine. An algorithm is simply a set of steps or instructions that can be followed to solve a problem.
In computer science, algorithms are used to perform various tasks, such as searching for information, sorting data, and optimizing processes. The purpose of an algorithm is to take input data and transform it into an output that satisfies the desired criteria. In order to do this effectively, algorithms need to be designed in a way that is both efficient and accurate.
Efficiency is an important aspect of algorithms, as the goal is to find a solution to a problem as quickly as possible. To achieve this, algorithms can use various techniques, such as reducing the number of steps required to solve the problem, or using more efficient data structures to store and process the data.
Accuracy is also an important factor in algorithm design, as the output of the algorithm must meet the desired criteria. This can be achieved by ensuring that the algorithm is well-structured, and that it uses appropriate data structures and operations to produce the desired results.
There are many different types of algorithms, each with its own strengths and weaknesses. Some algorithms are designed to solve specific types of problems, such as sorting or searching, while others can be applied to a wide range of problems. Some algorithms are also designed to run on large datasets, while others are designed to handle small amounts of data.
One of the most important aspects of algorithm design is choosing the right algorithm for the task at hand. This requires an understanding of the problem to be solved, as well as an understanding of the different algorithms that are available. The choice of algorithm will depend on a number of factors, such as the size of the data to be processed, the complexity of the problem, and the desired level of accuracy.
In conclusion, algorithms are an essential part of computer science, and they play a crucial role in solving problems efficiently and accurately. Whether you are working in a specific field or just looking to improve your problem-solving skills, understanding algorithms and how to use them effectively can be a valuable asset.

Big O

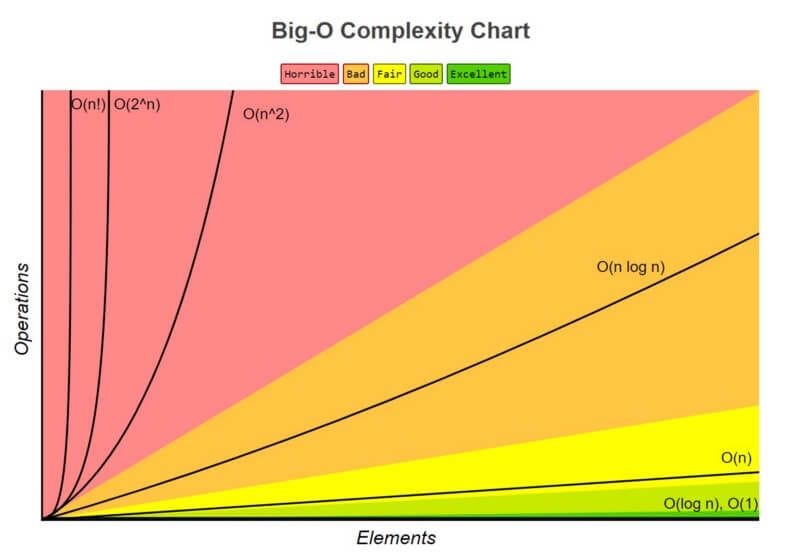Big O notation is a mathematical notation that is used to describe the upper bound on the growth rate of the running time of an algorithm. It is used to analyze and compare the performance of different algorithms in computer science.
Big O notation expresses the relationship between the size of the input and the number of operations required to solve the problem for that input. The size of the input is usually expressed as “n” and the number of operations is represented by the letter “O”. The term “Big O” is used to indicate that the number of operations grows at most as fast as the function O(n).
For example, if we have an algorithm that takes n steps to solve a problem of size n, we would say that the algorithm has a time complexity of O(n). This means that as the size of the input grows, the number of operations grows at most linearly with n.
Some common time complexities in Big O notation include:

• O(1): Constant time complexity, meaning the number of operations does not depend on the size of the input.
• O(log n): Logarithmic time complexity, meaning the number of operations grows logarithmically with n.
• O(n): Linear time complexity, meaning the number of operations grows linearly with n.
• O(n log n): Log-linear time complexity, meaning the number of operations grows as n log n.
• O(n²): Quadratic time complexity, meaning the number of operations grows as n squared.
• O(2^n): Exponential time complexity, meaning the number of operations grows exponentially with n.

It is important to note that Big O notation only provides an upper bound on the growth rate of the running time of an algorithm and does not describe the exact running time. Additionally, Big O notation only considers the dominant term in the growth rate, ignoring constant factors and lower-order terms.
In conclusion, Big O notation is a valuable tool for analyzing and comparing the performance of algorithms in computer science. It provides a way to express the relationship between the size of the input and the number of operations required to solve a problem, allowing us to compare the efficiency of different algorithms.