42 really is the answer to these 5 fundamental questions

Although we still don't know the question, we know that the answer to life, the Universe, and everything is 42. Here are 5 possibilities.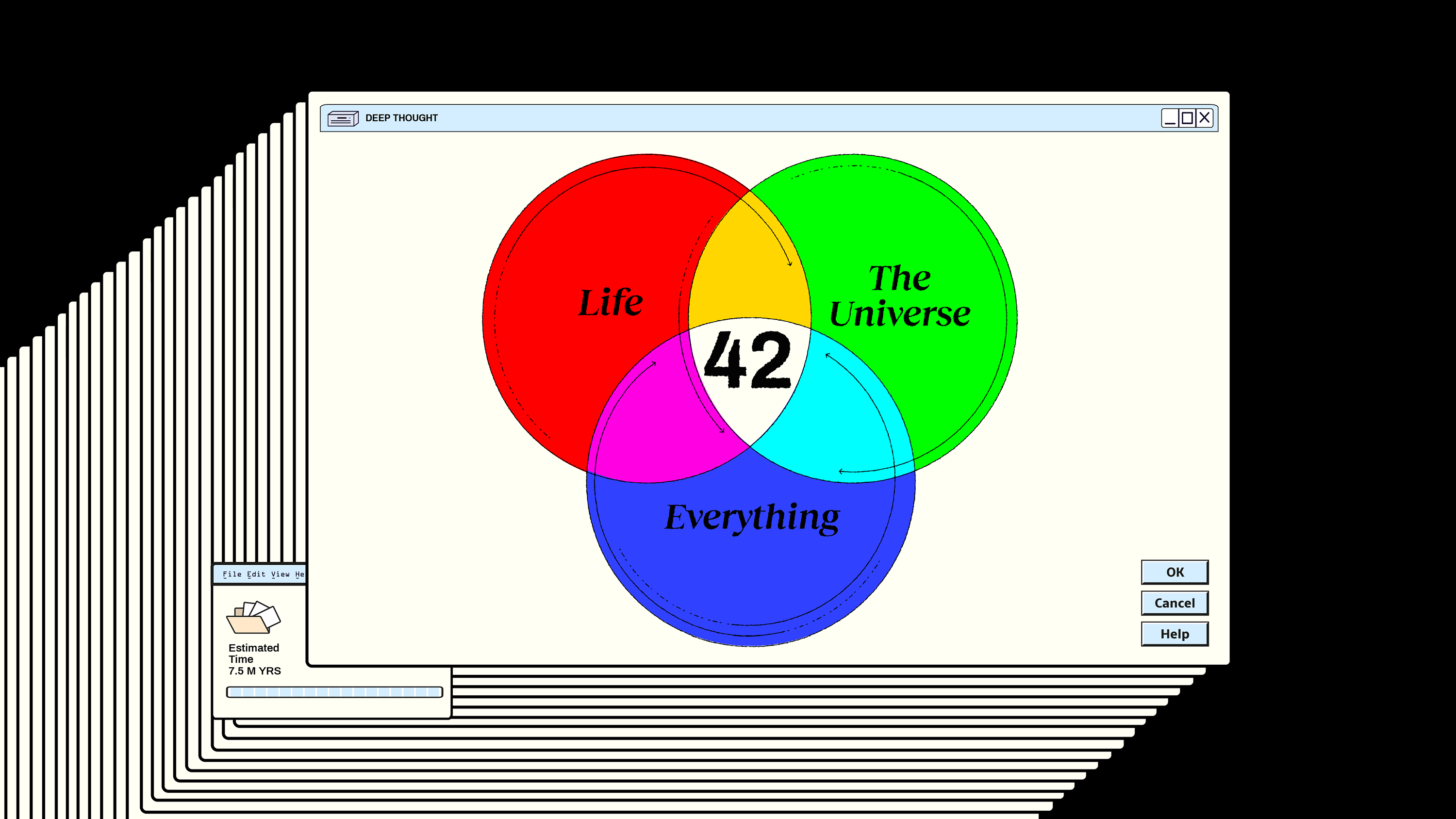

The answer to the ultimate question about life, the Universe, and everything has been asserted to be 42 by the infamous Douglas Adams. But... if 42 is the answer, what's the question?

KEY TAKEAWAYS

• If you programmed the ultimate supercomputer to give the answer to the ultimate question in the Universe, legend has it that, after 7.5 million years, the answer would at last be revealed: 42. Only, what's the point of knowing the answer if, 7.5 million years later, no one can remember what the question was? That paradoxical scenario is exploited for humorous effect in Douglas Adams' Hitchhiker's Guide series. Fortunately, modern physics and mathematics offers 5 extremely interesting, quite fundamental questions to which 42 really is the answer. Now, if only we can figure out which one to choose!

One of the most amusing stories in all of science fiction can be found within Douglas Adams’ The Hitchhiker’s Guide to the Galaxy, where a supercomputer is tasked with uncovering “the answer.” Allegedly designed to give the answer to the ultimate question about life, the Universe, and everything, the computer spends 7.5 million years calculating what the answer would be, and finally spits it out: 42. Only, when the answer is finally revealed, no one can remember what “the ultimate question” actually was. It’s another example of being so obsessed with getting to the destination that, upon reaching it, it no longer matters if you lost sight of the whole point of the journey to begin with.

Universe's beginning

Fortunately for us, there are a number of possible candidate questions — in hindsight — that we can exploit for their potential to truly be the ultimate question, given the fact that we know the solution is truly 42. Could any of these possibilities have truly been what the supercomputer was asked about when it came to uncovering the answer to the ultimate question about life, the Universe, and everything? Although no one can be sure, even in Douglas Adams’ fictional world, here are five possible questions that rank among the most fascinating. The answer to each of them truly is 42, and perhaps you might find one of them to be truly compelling.
As photographed from an airplane, direct sunlight shining on a “wall of water droplets” produced by rain clouds can not only produce a full-circle primary rainbow, but a full-circle secondary as well, creating a circular double rainbow. A primary rainbow, created when a light source shines on water droplets, always creates a 42 degree arc, offset with respect to the light source that creates it. A secondary rainbow can be seen above it as well with a larger-angle offset. The 42 degree angle is universal to rainbows created in air by fresh water droplets.

1.) At how many degrees, offset from the Sun (or any light source), is a rainbow produced?
There are many ways to create a rainbow: from raindrops to waterfalls to garden hoses to mist to the spray from bodies of water. Yet all of them have a few things in common. They all arise from light reflecting off of water droplets. They all originate in a direction that opposes the direction of a light source. And they all — so long as they’re created from droplets of fresh water — have a peak intensity spread out in an arc-like shape, a shape that’s actually a fraction of a full circle, which is offset 42° from the direction of the light source.

Every primary rainbow you’ve ever seen displays the same angle-of-arc. If there’s a rainbow that the Sun is creating, looking exactly opposite to the direction of the Sun and look for a circle (or portion of a circle) that’s offset from that direction by 42° will enable you to see it. The reason is simple physics: light behaves as a ray, the speed of light in water is different than the speed of light in air, and when light enters or leaves that medium, it always bends in a predictable way determined by the angle-of-incidence at the interface between the water and the air.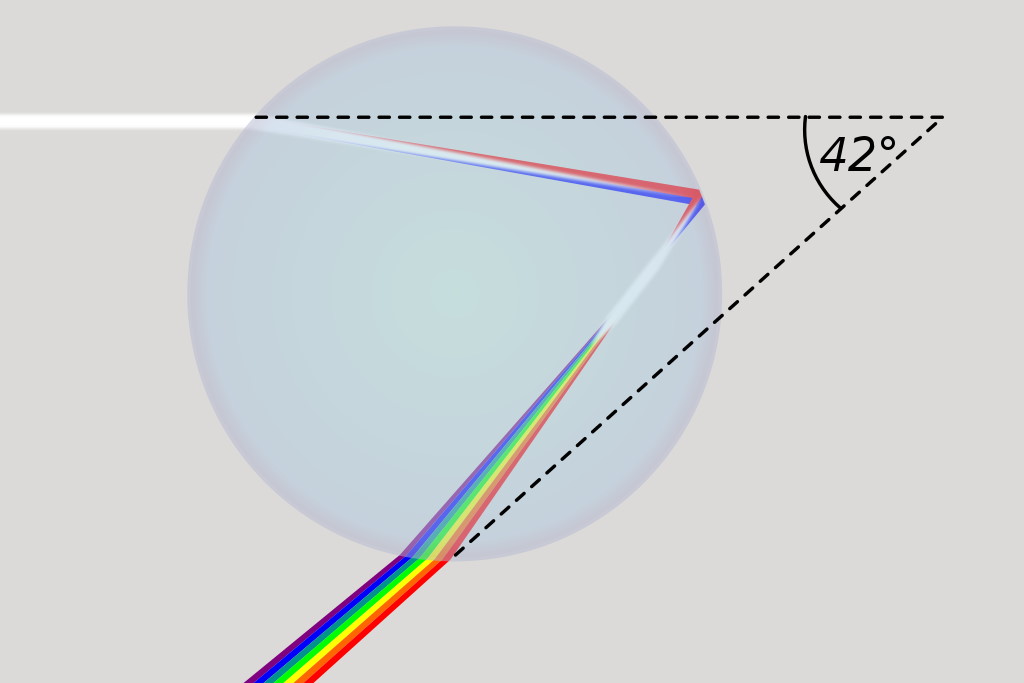
When light transitions from vacuum (or air) into a water droplet, it first refracts, then reflects off of the back, and at last refracts back into vacuum (or air). The angle that the incoming light makes with the outgoing light always peaks at an angle of 42 degrees, explaining why rainbows always make the same angle in the sky.
Credit: KES47/Wikimedia Commons
When light moves from air into water, different wavelengths bend at slightly different angles, causing the colors to disperse. When light strikes the back of the water droplet (and it’s a very good assumption that all droplets are perfectly spherical), it reflects at a known, predictable angle. And when it re-emerges back into the air, each wavelength moves off at a specific angle-of-offset from the original: from just under 41° to a little under 43° over the visible light spectrum, with the peak intensity occurring at 42°.

Any planet that possesses:

• a thin atmosphere,
• that’s transparent to visible light,
• where light travels at close to the speed of light in a vacuum,
• and where pure water droplets exist in the atmosphere,

will see that same 42° rainbow phenomenon. However, it’s not truly universal: if the atmosphere has a non-negligible index of refraction, if droplets are elliptical instead of spherical, if they’re made of saltwater instead of freshwater, if they’re made of a different substance entirely, or if the species viewing the rainbow doesn’t see the same wavelengths of light that we do, then the rainbow can occur at an entirely different angle.
Perhaps these limitations imply that we should consider a different candidate question instead.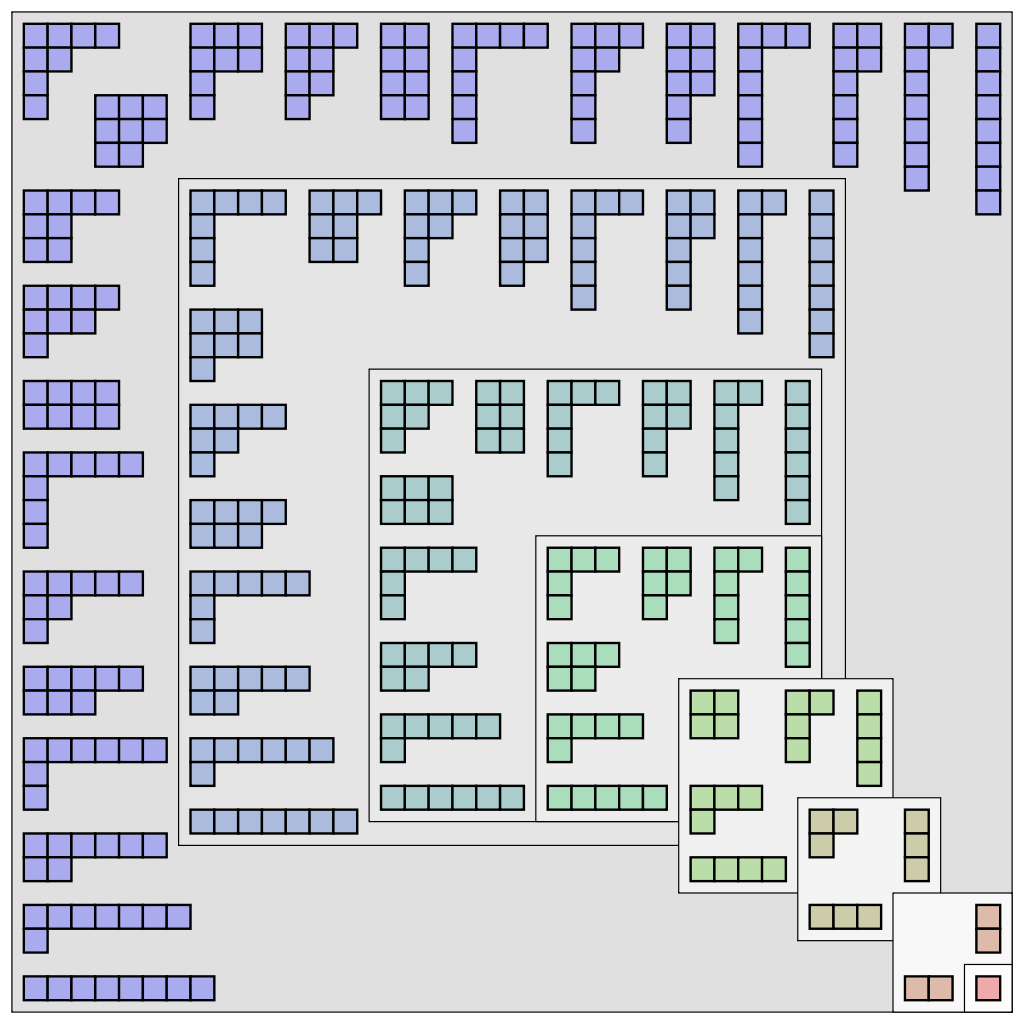
These diagrams, known as Young diagrams, show how to partition various numbers mathematically. (This shows the partitions for numbers 1 through 8.) For the number 1, there is 1 way to partition it (1); for 2, there are 2 (2, 1+1); for 3, there are 3 (1+1+1, 1+2, 3), but for 4 there are 5, for 5 there are 7, etc. Going farther up the ladder, there are exactly 42 unique ways to partition the number 10.

2.) What is the number of ways that you can partition the number 10?
It’s easy to think of different ways to divide up any number. If you have three oranges, and two people, for example, you can give all three to person 1, all three to person 2, one to person 1 and two to person 2, or 1.5 to each of the two people. In mathematics, however, partitioning has a very special meaning: how many unique ways can you add up positive integers to create a certain number? Positive integers means that no one can get zero or a fractional number; unique means that splitting things up into “2 and 1” is the same as splitting them into “1 and 2.”

For an example of partitioning, there are 7 ways to partition the number 5:

• 1 + 1 + 1 + 1 + 1,
• 1 + 1 + 1 + 2,
• 1 + 1 + 3,
• 1 + 2 + 2,
• 1 + 4,
• 2 + 3,
• 5.

For the number 10, with all the different ways to do it, there are a total of 42 unique ways to do it. Fascinatingly, this isn’t the only relationship between 10 and 42, as 10 can be written as 2¹ + 2³, while 42 can be written as 2¹ + 2³ + 2⁵. If we were to write these numbers in binary, “10” would become 1010, while “42” would become 101010. These numbers and these relationships play important roles in both mathematics and physics (particularly through group theory), with 42 having some fascinating properties completely independent of any measured physical phenomena.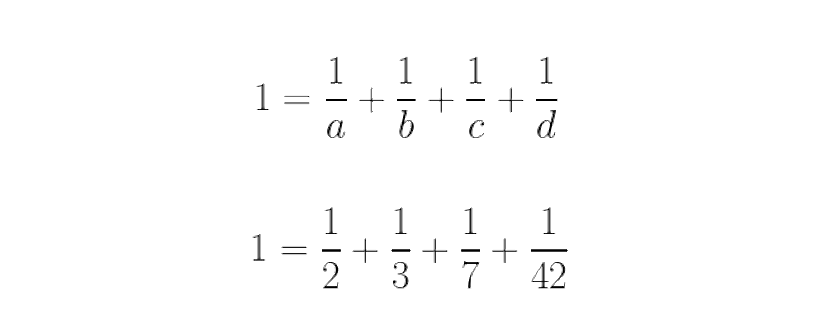
The equation 1 = 1/a + 1/b + 1/c + 1/d only has a few unique solutions if a, b, c, and d are all different, positive integers. The largest number for which there exists a solution to this equation, perhaps surprisingly, is the number 42.
Credit: E. Siegel/LaTeX
3.) What is the largest integer whose reciprocal, along with three other unique integer reciprocals, adds up to 1?
Perhaps the Universe, as some have conjectured, really is driven by mathematical relationships at a core level, with those relationships underpinning the physical laws of reality. For those of you who think that might be the case, here’s a math puzzle for you to consider:

Can you find four positive integers, like a, b, c, and d, where (1/a) + (1/b) + (1/c) + (1/d) = 1?
It’s easy to do if you make certain choices. For example, if a, b, c, and d all equal 4, this is very simple, as ¼ + ¼ + ¼ + ¼ = 1. If you even allow just some of the numbers (a, b, c, d) to be equal, there are many possible solutions:

• a=2, b=4, and c=d=8;
• a=b=3, c=4, d=12;
• a=2, b=c=d=6;

and so on.
But if you insist that all four of these numbers must be different from one another, there are very few unique solutions. In fact, you can work out the math to find the absolute the largest number that you can use to try and satisfy this equation that will still give you a solution.
The answer? 42.
If you let a=2, b=3, and c=7, then d=42 and the equation works. Interestingly enough, that’s not the only relationship between those four numbers, as 2, 3, and 7 are the prime factors of 42: 42 = 2 × 3 × 7. In even a purely mathematical sense, 42 has some truly fascinating properties.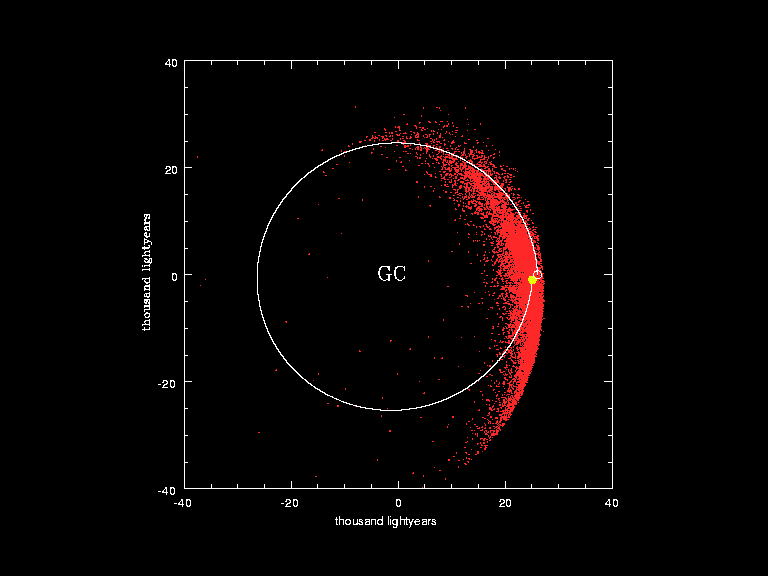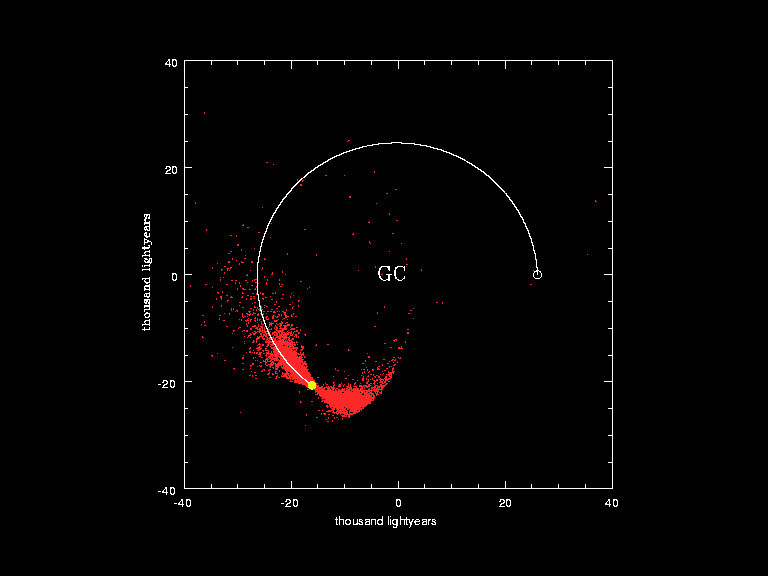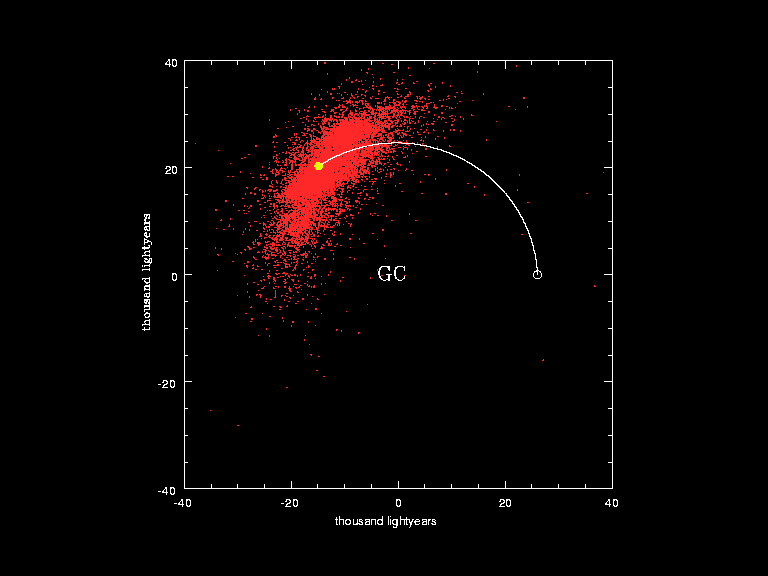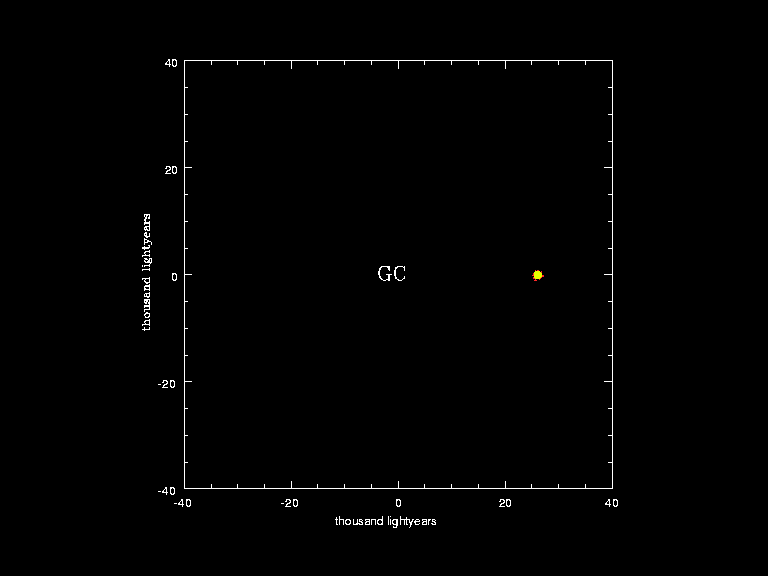
A 15-year study conducted by the European Southern Observatory tracked the positions and orbital parameters of 14,000 stars near the Sun, reconstructing how they would have orbited, along with the Sun, over the past 250,000,000 years: the amount of time to complete approximately 1 galactic year. The position of the galactic center does not change relative to the motion of stars around it, and our Sun’s orbit is notably elliptical, rather than perfectly circular.
Credit: ESO, European Southern Observatory
4.) How many times will the Sun orbit the Milky Way before catastrophically transforming into a red giant?
This is one of the most fun facts about our Solar System, where the planets revolve around the Sun and the Sun, like all stars, orbits around center of the Milky Way. Like all stars, there’s only a finite amount of time that the Sun will live, with various milestones marking its critical transitions. It takes tens of millions of years for the proto-stellar nebula that gives rise to our Solar System to form our Sun, which officially becomes a star once nuclear fusion of hydrogen into helium ignites in its core.

After that, the Sun will chug along for billions of years until the core runs out of hydrogen fuel, at which point it will begin to swell into a red giant, burning hydrogen in a shell until the helium core ignites. During this phase, Mercury and Venus will certainly be engulfed, and it’s likely (but not certain) that the Earth will be swallowed as well. Icy worlds, like Triton, Pluto, and most of the Kuiper belt objects, will sublimate away almost entirely. This red giant phase will last for hundreds of millions of years while helium burns to completion. At that point, the Sun will blow off its outer layers, dying in a planetary nebula/white dwarf combination.
As the Sun becomes a true red giant, the Earth itself may be swallowed or engulfed, but will definitely be roasted as never before. The Sun’s outer layers will swell to more than 100 times their present diameter, but the exact details of its evolution, and how those changes will affect the orbits of the planets, still have large uncertainties in them. Mercury and Venus will definitely be swallowed by the Sun, but Earth will be very close to the border of survival/engulfment.

Yet, throughout all of these changes, the Sun and our Solar System will continue to orbit around the Milky Way’s center, completing a full orbit every ~250 million years or so. The time to return to our starting point is known as a galactic year, and has about a ~10% uncertainty on how long it actually takes. Meanwhile, in term of stellar evolution, we are quite confident that the Sun will last roughly 10–12 billion years from the moment nuclear fusion first ignites in its core until the red giant phase begins, a track that we’re just a hair over 4.5 billion years into, at present.
So, how many galactic years will the Sun (and Earth) experience before the Sun swells into a red giant and planet Earth is (likely) completely destroyed?
42.
Although justifiable estimates typically range from about 40 to 45 — driven largely by an approximately ~10% uncertainty in how fast the Sun is orbiting around the Milky Way’s center — 42 is an answer that’s extremely consistent with the best data we have. It may yet turn out to be the exact answer to this question, although superior data will be required to know for certain.
However, that’s an Earth-centric perspective, and perhaps we’d want to look to the greater Universe for an even grander question to consider.
The European Space Agency’s space-based Gaia mission has mapped out the three-dimensional positions and locations of more than one billion stars in our Milky Way galaxy: the most of all-time. From the best measurements of our own galaxy, we estimate that it takes approximately 250 million years for the Sun to complete one revolution around the Milky Way, with an estimated 40-45 revolutions likely during the main sequence lifetime of our Sun.
ESA/Gaia/DPAC
5.) How fast is the Universe expanding today?
Right now, we exist in the Universe precisely 13.8 billion years after the earliest stages of the hot Big Bang occurred. For all of cosmic time, the Universe has been expanding and cooling, and that means it’s been getting less dense. In the expanding Universe, the thing that determines your expansion rate is the density of all the different forms of energy combined, so an expanding Universe filled with matter and radiation will have the expansion inevitably slow down over time.
Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

Fields marked with an * are required

The expansion rate, today, is slower than it’s ever been at any time in the past, and continues to gradually slow down. If we wait for a long enough time, the matter and radiation density will drop to zero, with only dark energy — the energy inherent to space itself — remaining. By convention (and for no other reason), we typically report the expansion rate as a speed (how fast something appears to be moving) per unit distance (based on how far away it is from us): in units of kilometers-per-second, per megaparsec.
This graph shows the 1550 supernovae that are a part of the Pantheon+ analysis, plotted as a function of magnitude versus redshift. The supernova data, for many decades now (ever since 1998), has pointed toward a Universe that expands in a particular fashion that requires something beyond matter, radiation, and/or spatial curvature: a new form of energy that drives the expansion, known as dark energy. The supernovae all fall along the line that our standard cosmological model predicts, with even the highest-redshift, most far-flung type Ia supernovae adhering to this simple relation.
D. Brout et al./Pantheon+, ApJ submitted, 2022
In those units, we have two classes of measurements that point to inconsistent values: measurements that are based on relics imprinted from early times, like fluctuations in the cosmic microwave background or galaxy clustering in the large-scale structure, and measurements that come from individual sources at late cosmic times, like supernovae or gravitational lenses. The first set of measurements yields a value of 67–68 km/s/Mpc, while the second yields a value of 73–74 km/s/Mpc. Figuring out what the resolution to this puzzle is — i.e., which group is correct, and why — is one of modern cosmology’s biggest challenges.
But if the first group is right, then perhaps the answer to the question of how fast the Universe is expanding really is 42.
That’s because we have to remember this fact: Douglas Adams was writing in 20th century England, where distances are measured in miles, not kilometers! If we perform that conversion, from kilometers into miles, then that first value of the expansion rate, which was 67-68 km/s/Mpc, becomes 42 mi/s/Mpc, which could easily be construed as the answer to the biggest question in entire cosmos: how fast is the Universe expanding right now? Although more science will be required to truly resolve this cosmic conundrum, “42” is well within the realm of possible — and may even be the most probable of — answers.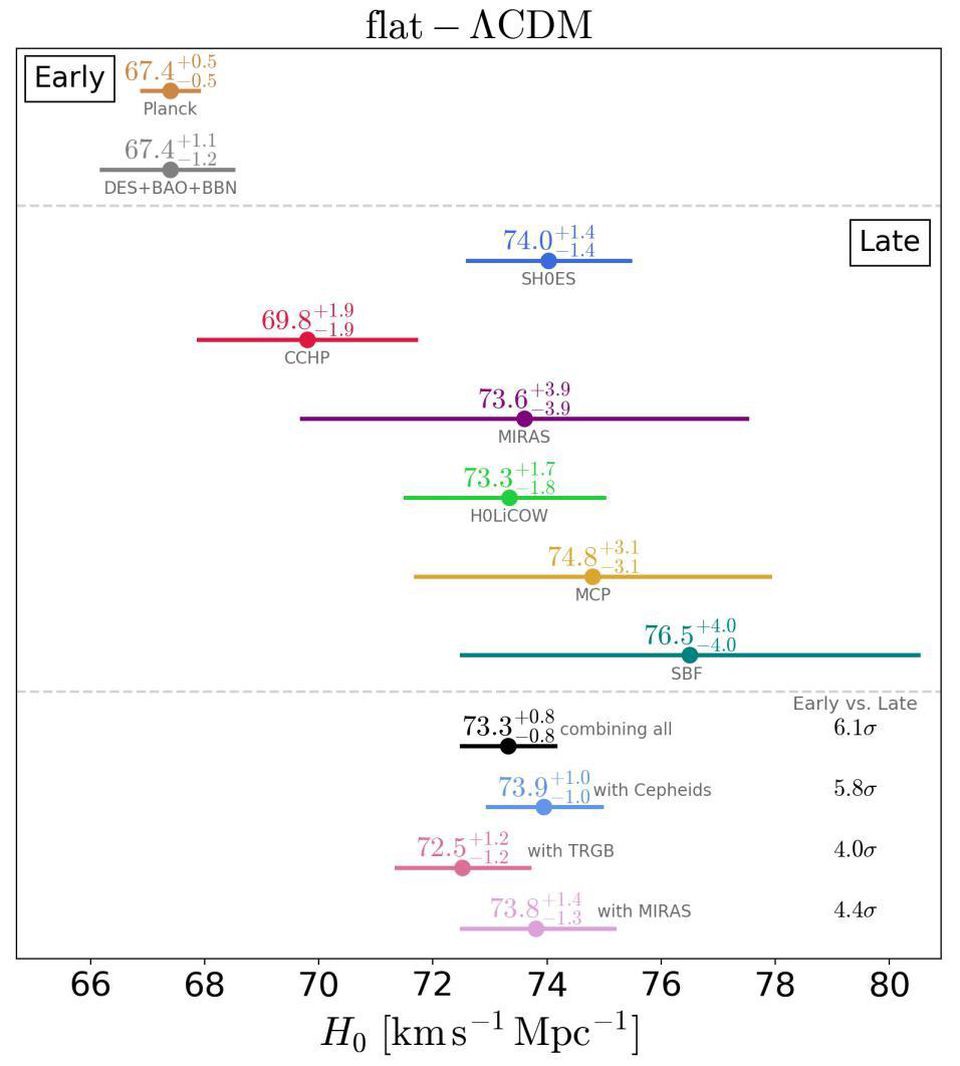
A series of different groups seeking to measure the expansion rate of the Universe, along with their color-coded results. Note how there’s a large discrepancy between early-time (top two) and late-time (other) results, with the error bars being much larger on each of the late-time options. Although these two classes of measurements give incompatible results, no one knows the resolution to why the Universe appears to expand differently dependent on the method used to measure the expansion.
L. Verde, T. Treu & A.G. Riess, Nature Astronomy, 2019
All told, there are many questions that 42 is clearly the answer to, but only a few of those questions have fundamental, universal, or cosmic implications. If it truly is the answer to the ultimate question about life, the Universe, and everything, we owe it to ourselves to try and reconstruct just what that question might be. From mathematics to physics, five vital questions emerge that legitimately have 42 as their answer.

• Rainbows always emerge offset at an angle of 42° relative to the light source that creates them.
• The number 10 can be mathematically partitioned exactly 42 different ways.
• 42 is the largest number whose reciprocal, added with three other unique positive integers, sums to exactly 1.
• 42 is the number of galactic years that the Sun-Earth system will survive before it’s destroyed.
• And 42 is the expansion rate of the entire Universe, in miles-per-second-per-megaparsec.

As it turns out, “42” really could be the answer to the vaunted ultimate question about life, the Universe, and everything. Now, it’s up to us to figure out what that pesky, ultimate question actually is!