Understanding Hooke's Law of Elasticity: A Fundamental Principle in Material Science

Introduction:
Hooke's Law of Elasticity, formulated by Robert Hooke in the 17th century, remains a cornerstone in the field of material science and engineering. This law describes the linear relationship between the force applied to an elastic material and the resulting deformation. This essay explores the historical context, the mathematical formulation, applications, limitations, and modern implications of Hooke's Law, emphasizing its enduring relevance in various fields.
Historical Context:
Robert Hooke, an English scientist and polymath, formulated Hooke's Law in 1660 while working on his pioneering studies in microscopy and mechanics. In his seminal work "Micrographia," Hooke presented his observations on the behavior of springs and proposed the linear relationship between force and displacement. The law was first expressed as "ut tensio, sic vis" which translates to "as the extension, so the force" in Latin, encapsulating the essence of the relationship he observed.
Mathematical Formulation:
Hooke's Law is mathematically expressed as:

F=k⋅x
Where:

• F is the force applied to the material
• k is the spring constant (also known as the stiffness constant) of the material,
• x is the displacement or deformation from the material's equilibrium position.

This equation signifies that the force exerted on a material is directly proportional to the amount of deformation caused by the applied force, as long as the material remains within its elastic limit.
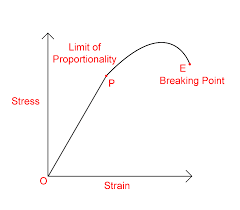
The graph:
Applications:
Hooke's Law finds widespread applications across various disciplines, including:
1. Mechanical Engineering:
It forms the basis for designing and analyzing mechanical systems involving springs, such as suspension systems in vehicles and mechanical watches.
2. Material Science:
It helps characterize the mechanical properties of materials, facilitating the design of structures and materials with desired elastic behavior.
3. Civil Engineering:
Hooke's Law is utilized in analyzing the behavior of structural elements like beams and columns under different loading conditions.
4. Biomechanics: It is employed to understand the mechanical properties of biological tissues and to design prosthetics and orthopedic devices.
5. Geophysics: Hooke's Law assists in studying the elastic properties of rocks and understanding seismic wave propagation in the Earth's crust.
Limitations:
While Hooke's Law provides a useful approximation for many materials under small deformations, it has certain limitations:

1. Validity: Hooke's Law is strictly valid only within the material's elastic limit. Beyond this limit, materials exhibit nonlinear behavior, such as plastic deformation or fracture.
2. Material Dependency: Different materials have different stiffness constants, and Hooke's Law may not accurately describe the behavior of materials with complex internal structures or non-linear elastic behavior.
3. Temperature Sensitivity: The stiffness of materials can be temperature-dependent, leading to deviations from Hooke's Law at extreme temperatures.
4. Time Dependency: Some materials exhibit time-dependent deformation (creep) under sustained loads, which is not accounted for in Hooke's Law.

Modern Implications:
In contemporary research and engineering, Hooke's Law continues to play a crucial role:

1. Nanotechnology: With advancements in nanoscale materials and devices, understanding the elastic behavior of nanomaterials is essential for developing novel applications in electronics, medicine, and energy.

1. Smart Materials: Hooke's Law inspires the development of smart materials with tunable mechanical properties, enabling applications in adaptive structures, robotics, and biomedical devices.
2. Computational Modeling: Hooke's Law serves as a fundamental principle in computational modeling techniques such as finite element analysis (FEA), aiding in the virtual prototyping and optimization of complex systems.

1. Materials Design: Researchers leverage Hooke's Law to design and engineer materials with tailored elastic properties for specific applications, such as lightweight composites for aerospace or high-strength alloys for automotive components.

Conclusion:
Hooke's Law of Elasticity stands as a foundational principle in material science and engineering, providing a simple yet powerful framework for understanding the behavior of elastic materials under external forces. Despite its age, Hooke's Law remains highly relevant in modern research and technology, serving as a guiding principle in diverse fields ranging from mechanical engineering to nanotechnology. As technology advances and our understanding of materials deepens, Hooke's Law continues to inspire innovation and drive progress in science and engineering.
References:

1. Hooke, R. (1660). Micrographia.
2. Timoshenko, S. P., & Goodier, J. N. (1970). Theory of elasticity. McGraw-Hill Education.
3. Love, A. E. H. (1927). A treatise on the mathematical theory of elasticity. Cambridge University Press.
4. Suresh, S. (2006). Fatigue of materials. Cambridge University Press.
5. Gibson, L. J., & Ashby, M. F. (1997). Cellular solids: structure and properties. Cambridge University Press.