DETERMINATION OF THE FLOW REGIME
1. Purpose In chemical processes, fluids have to pass through pipes, channels and the equipment where the process is carried out. In this experiment, it is aimed to determine the laminar and turbulent flow regime of an incompressible fluid in an open channel and to measure the average velocity and center velocity by measuring the flow rate.
Learning outcomes
Flow regimes are visually examined by working at different flow rates.
Knows how Reynolds number, flow rate and speed values are measured and the theory on which they are based,
Uses an experimental system safely,
2. General Information
Laminar Flow
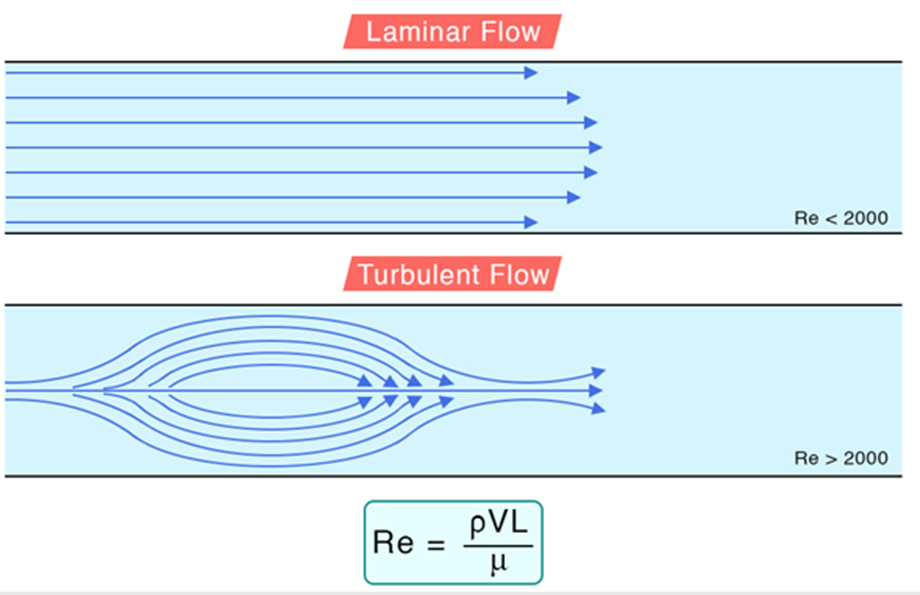
While some flows are quite turbulent, others are smooth and orderly. Very regular flow motion indicated by smooth streamlines is called laminar flow. At low speeds, the motion of high viscosity fluids such as oil is generally laminar. Laminar flow is the flow of fluid in parallel and uniform layers.
Turbulent Flow
Highly disordered fluid motion generally occurs at high velocities and is indicated by flow changes called turbulence. Turbulent flow is the flow of fluid in irregular, cross-flows and eddies. At high speeds, the movement of low-viscosity fluids such as air is often turbulent. The flow regime significantly affects the power required to pump the fluid.
Transition Zone
The transition from laminar to turbulent flow does not occur suddenly. Instead, this transition occurs in some regions of the flow where it alternates between laminar and turbulent flow before the flow becomes fully turbulent. Most flows encountered in practice are turbulent. Laminar flow is encountered when viscous fluids such as oil flow through small pipes or narrow passages.
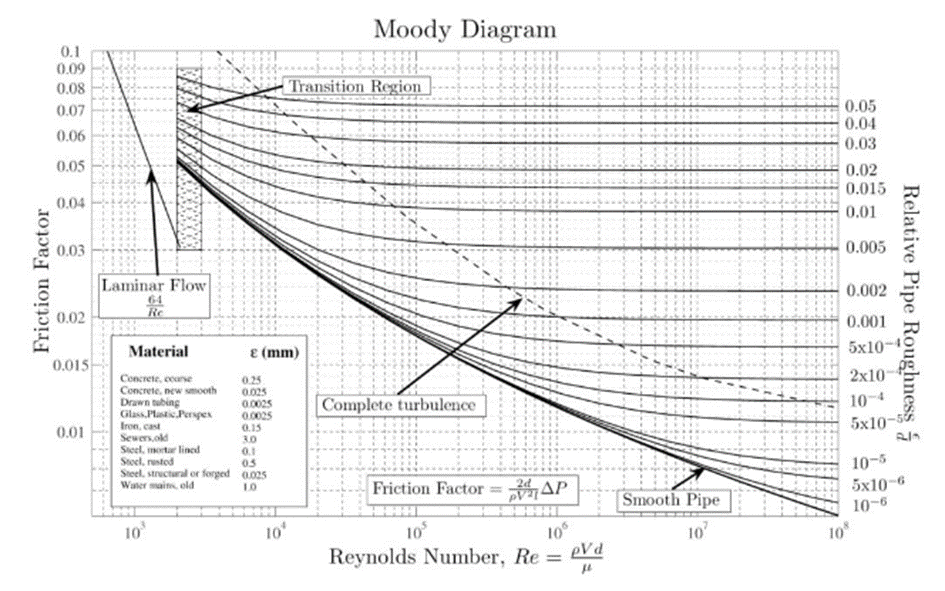
Reynolds Number The flow of a fluid in a pipe can be laminar or turbulent flow. The transition from laminar to turbulent flow depends on geometry, surface roughness, flow rate, surface temperature, and fluid type, among other factors. After detailed experiments, the British scientist Osborne Reynolds (1842-1912) found that the flow regime depends mainly on the ratio of inertial forces to viscous forces in the fluid.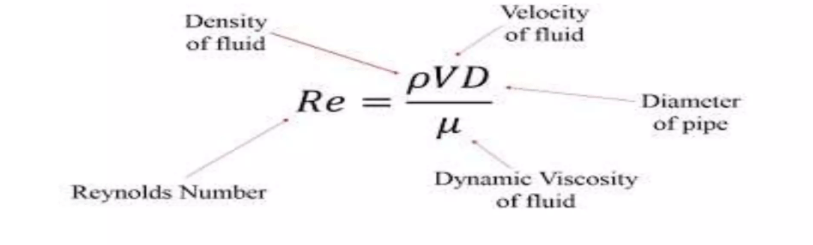
This ratio is called Reynolds number. The dimensionless number, called the Reynolds number, is defined as Re = ρVL/µ. Here, L is a length characterizing the flow, and in the case of a circular cross-section pipe, it is equal to the pipe diameter D. In pipes and channels that are not circular in cross-section, the hydraulic diameter expressed as Dh is used instead of D. The hydraulic diameter is defined as Dh = 4A/Ç, where A indicates the cross-section of the pipe or channel perpendicular to the flow and Ç indicates the environment wetted (licked) by the flow. V refers to the average flow velocity (= m/ ρA), m is the mass flow rate of the flow, and ρ and μ are the density and dynamic (absolute) viscosity of the fluid, respectively.
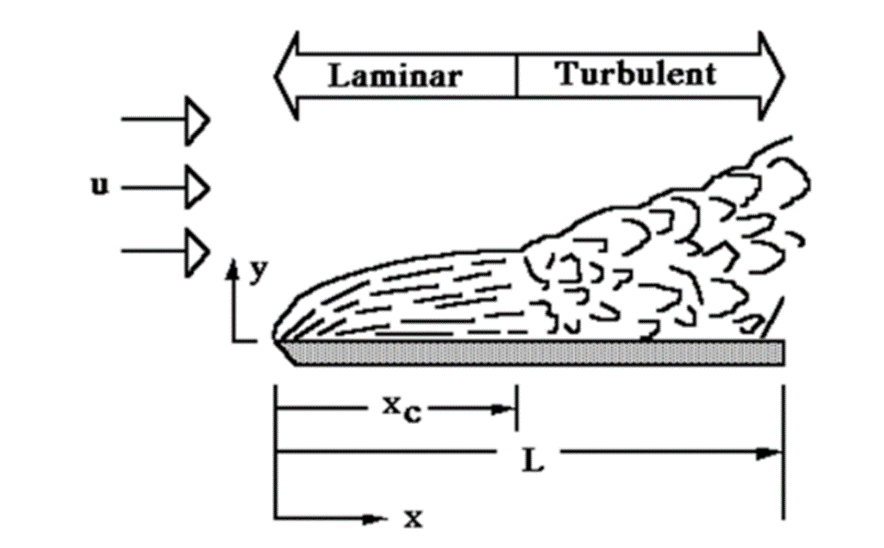
The magnitude of the Reynolds number does not depend on units, provided the units used are compatible with each other. The transition from laminar to turbulent flow can occur over a range of Re numbers. In laminar flow, the Re number is usually less than approximately 2100. Under normal flow conditions, the flow is turbulent at values of Re greater than approximately 4000. At values of Re number between 2100 and 4000, depending on the inlet conditions, the flow pattern is neither fully laminar nor turbulent, and the flow in this range is generally called the transition zone. The development of the flow and velocity profile in a tubular flow is shown in Figure 1. In this way, when the fluid entering a circular pipe comes into contact with the walls, due to the non-slip condition, the speed at the walls becomes zero and the speed increases as it moves away from the walls towards the center of the pipe. As a result, a velocity profile varying in the r direction is formed in any section of the pipe. The velocity profile is the graph that shows the change of local velocities with distance in the direction perpendicular to the surface. The region between the wall and the flow where local velocities change is called the boundary layer.
Figure 1. Velocity profiles and velocity development in a circular cross-section pipe. Up to a certain distance in the flow direction in the pipe, the shape of the velocity profiles changes in the x direction until the velocity change reaches the center. Then the shape of the velocity profiles remains constant and does not change in the flow direction. The region where the velocity profiles change in the x direction is called hydrodynamically developing flow, and the region where it remains constant is called fully developed flow. For laminar flow, the length of the hydrodynamic entrance region is calculated from the following equation: , (laminer/d ≅0.05Re) For turbulent flow, the length of the fully developing region is taken as approximately 10 pipe diameters.
Flow Regimes
A typical velocity distribution for a Newtonian fluid flowing with laminar and turbulent flow in a smooth pipe is shown in Figure 2. The figure also shows velocity regions in the same turbulent flow. The dispersion curve for turbulent flow appears to be a wider parabola than that for laminar flow. At the same time, the difference between maximum speed and average speed is smaller.
In laminar flow, the flow is laminar across the entire cross-sectional area of the pipe. In a very thin layer near the solid surface, the flow is very slow and the flow regime is laminar. The vortex rarely reaches this layer. This layer, which has a certain thickness and a laminar feature with no permanent vortices, is called the viscous sublayer. The viscous substrate occupies only a small part of the flow cross section. The viscous substrate thickness at any point changes with time due to the effect of vortices of different sizes on the viscous substrate. In the viscous substrate, only viscous friction is important. Between the viscous bottom layer and the turbulent center, there is a transition layer in which there is both viscous friction and vortex friction. This transition zone is called the buffer zone and is a relatively thin layer. The remaining flow area is occupied by the flow called the turbulent center. Viscous shear within the turbulent center is neglected compared to shear due to turbulent viscosity. Figure 3 shows the dye trace in the Reynolds test and flow regimes schematically.